









































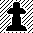




















[Next]
- #1
- This is a difficult endgame that is
- found in many endgame books including
- "Essentail Chess Endings Explained
- Move by Move" by Silman which I
- recommend.










































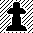





















[Next]
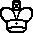
- #1
- The key to this position is that if
- White can reach e2 then he will win.
- But if the white king were to march
- over toward e2 then the black king
- has time to get to e3 and stop the
- white king from getting to e2....










































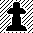





















[Next]
- #1 continued.
- But if we go back to the original
- position....










































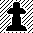





















[Next]
- #1
- And move the black king one square to
- the left .....










































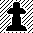





















[Next]
- #1 variant
- Now we calculate this position we see
- that White has time to reach e2 which
- will allow him to win the game.










































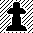





















[Next]
- #1
- So this means that when the White
- king in on a2 then the black king
- must be on b4 (and not a4!)
- That means the squares a2 for the
- white king and b4 for the black king
- are "corresponding."
- By that we mean that if black wants
- to draw he has to be able to move to
- the corresponding square of b4 just after
- white moves to the corresponding square of
- a2.
- (Note that if the White king gets to
- b3 then he wins. So it is up to the
- Black king to stop that by going to
- b4.)










































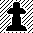





















[Next]
- #1 Variant
- But there are more "corresponding" squares
- than just a2 and b4. Black needs to
- be able to block the white king on
- both the a file and the e file.
- So the Black king must be able to get
- to the square c5 when the White king
- is on b1. If the black king is on
- any other square then
- he will lose because he cannot get to
- either the left or the right fast
- enough to stop white.










































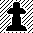





















[Next]
- #1 continued.
- Likewise the squares d4 is corresponding to
- c1. If the black king is on any
- other square he will lose the game.










































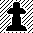





















[Next]
- #1 continued.
- The same can be said for d1 and e3.
- If black is on any other square he
- will lose becaue he will either not
- be able to stop Ke2 or not be able to
- stop the White king from marching
- over to b3.










































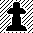





















[Next]
- #1 continued.
- This is where the position gets
- really interesting. White just moved
- to e1 and has the opposiiton.
- Where should Black move
- to?










































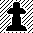





















[Next]
- #1 continued.
- The answer is that f3 is the only
- square black can now draw from. The
- reason for this is that black still
- needs to stop Ke2 while at the same
- time he needs to be able to go back
- to e3 after the White king goes back
- to d1.










































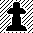





















[Next]
- #1 continued.
- This funny looking position sort of
- defies our common sense notions about
- how king and pawn endgames should
- work. We can ask ourselves the
- quesiton .....










































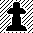





















[Next]
- ... Why can't black draw if his king
- is on e3 where he has opposition
- assuming it is white to move?










































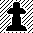





















[Next]
- The answer is that certain pawn
- formations can be like little "black
- holes" that distort "space." The
- normal squares of opposition really
- don't apply here. Black really has
- opposition when his king is on f3 and
- not e3.
- Watch what happens next ....










































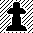





















[Next]
- The White king heads back toward b3
- and black has real delima here. If
- his king goes to d4 then he will lose
- because White will be able to play
- Ke2. So instead he has no choice to
- play ...










































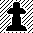





















[Next]
- ... Kf3. But this will lose because
- now the black king is too far away to
- get back to b4 in time to stop the
- White king from getting to b3 which
- will win easily.










































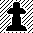





















[Next]
- #1
- If we look again at our original
- position, we can say that Black draws
- here if it is white's turn. In
- effect Black has "opposition" even
- though the normal rules of opposition
- squares have been distorted by the
- pawns. (Our "black hole" on the
- chess board.)










































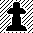





















[Next]
- #1
- If on the other hand it was Black's
- turn in this posiiton then he would
- lose the game because he would be
- forced to move out of his ideal
- square.
- So if it were black's turn to move
- then "white" would have opposition.
[Next]
 /
/